PGCD et nombres premiers:

a et b sont des nombres entiers différents de 0.

On dit que b est un diviseur de a, (ou que a est divisible par b)

si le quotient ^a/_b est un nombre entier.

Exemple:

4 est un diviseur de 16: ¹⁶/₄=4.

mots à utiliser :multiple, et diviseur.

Définition:

Un diviseur commun de a et de b est un nombre qui divise à la fois a et b.

Le plus grand de ces nombres est le Plus Grand Commun Diviseur de a et de b.

Il se note PGCD(a,b).

Exemple:

Diviseurs de 20: 1, 2, 4, 5, 10 et 20

Diviseurs de 8: 1, 2, 4 et 8

Donc le PGCD(20; 8) = 4.

Algorithme d'Euclide

Si un nombre est le PGCD de a et de b (avec a > b) alors c'est aussi le PGCD de b et du reste de la division euclidienne de a par b.

On effectue une série de divisions euclidiennes.

On arrête l'algorithme quand on obtient un reste égal à 0.

Le PGCD est le dernier reste non nul.

A = B×q + r

B = r×q₁ + r₁

r = r₁×q₂ + r₂

r₁ = r₂×q₃ + r₃

r_n-1 = r_n×q_n+1 + r_n+1

Clique sur le bouton "`Lance l'algorithme" et donne une valeur à a et à b

Exemple:

PGCD(252; 168) = 84

Preuve:

252 = 1×168 + 84

168 = 2×84 + 0

Dernier reste non nul: 84

Nombres premiers:

Deux nombres sont premiers entre eux si leur PGCD vaut 1.

Exemples:

1) 105 et 25 ne sont pas premiers entre eux car 105 et 25 sont divisibles par 5.

2) 23 et 17 sont premiers entre eux, PGCD(23; 17) = 1.

Fractions irréductibles:

Définitions:

1) On dit qu'une fraction est irréductible quand je ne peux plus la simplifier

2) Une fraction est dite irréductible quand son numérateur et sont dénominateur sont premiers entre eux.

3) Pour rendre irréductible une fraction ^a/_b (avec b≠0), il suffit de la simplifier par le PGCD(a; b).

Exemple:

Simplifie: ²⁵²/₁₆₈=^(3×84)/_(2×84)=³/₂.

Entraîne toi:

résultats à utiliser :⁶⁴/₉₃, ¹⁵/₁₃ et ⁷/₅.

Développement/Factorisation:

Définitions:

1) Développer un produit, c'est le transformer en une somme.

2) Factoriser une somme, c'est la transformer en un produit.

Règles:

Soient a, b, c, d et k quatre nombres, alors:

1) k×(a+b)=k×a+k×b.

2) k×(a-b)=k×a-k×b.

3) (a+b)(c+d)=a×c+a×d+b×c+b×d.

4) (a-b)(c-d)=a×c-a×d-b×c+b×d.

Dans l'exemple 4), on utilise la règle des signes.

Attention:Après avoir développé une expression, on la réduit.

Les identités remarquables:

résultats à utiliser :a²-b², a²-2a×b+b² et a²+2a×b+b².

Exemples:

1) (2x+1)²=(2x)²+2×2x×1+1²=4x²+4x+1.

2) (3x-8)²=(3x)²-2×3x×8+8²=9x²-48x+64.

3) (4x-3y)(4x+3y)=(4x)²-(3y)²=16x²-9y².

4) 25x²-40x+16=(5x)²-2×(5x)×4+(4)²=(5x-4)²

5) 9x²+36x+36=(3x)²+2×(3x)×6+(6)²=(3x+6)²

6) 25x²-16=(5x)²-(4)²=(5x+4)(5x-4).

Racines carrées:

Définition:

Pour tout nombre a positif, il existe un unique nombre positif dont le carré vaut a.

Ce nombre se note √a, on lit racine carrée de a et le symbole √ est appelé radical.

Si a≥0, (√a)²=a et √(a²)=a.

Propriétés:

2) Si a et b deux nombres psitifs tel que b;ne;0, alors: √(^a/_b)=^√a/_√b.

Exemples:

1) √75=√(3×25)=√3×√25=√3×√(5²)=5√3.

2) ^√75/_√3=√(⁷⁵/₃)=√25=√(5²)=5.

Entraîne toi:

résultats à utiliser :9√5, ⁶/₅ et 2√5.

En général:√(a+b)≠√a+√b

Exemple:

√(16+9)=√25=√(5²)=5

√16+√9=√(4²)+√(3²)=4+3=7.

Or 5≠7 et donc √(16+9)≠√16+√9.

Equations et inéquations du 1er degré:

Equations du 1er degré:

Résoudre une équation, c'est trouver toutes les valeurs numériques qui vérifient l'égalité.

Chacune de ces valeurs est appelée solution de l'équation.

1) L'équation a+x=b a pour solution x=b-a.

2) L'équation a×x=b a pour solution x=^b/_a si a≠0.

3) Si un produit de facteurs est nul, alors au moins l'un de ses facteurs est nul:

Inéquations du 1er degré:

Résoudre une inéquation, c'est trouver toutes les valeurs numériques qui vérifient l'inégalité.

Pour résoudre une inéquation, utilise les propriétés suivantes:

1) Si on ajoute un même terme aux deux membres d'une inégalité, alors l'inégalité ne change pas de sens.

2) Si on multiplie ou si on divise les deux membres d'une inégalité par un même facteur positif, alors l'inégalité ne change pas de sens.

3) Si on multiplie ou si on divise les deux membres d'une inégalité par un même facteur négatif, alors l'inégalité change de sens.

Exemples et méthodes:

1) Résoudre:3x-2=-2x+8.

Objectif: mettre les termes en x ensemble dans le membre de gauche et les constantes dans le membre de droite.

On obtient: 3x+2x=8+2 soit 5x= 10 ce qui donne x=¹⁰/₅=2.

Cette équation a une solution qui est le nombre 2.

2) Résoudre l'équation produit suivante: (2x-1)(4-3x)= 0.

Objectif: on résout séparément chacune de ces deux équations:

2x-1=0 ou 4-3x=0

soit x=¹/₂ ou x=⁴/₃.

Cette équation admet 2 solutions: les nombres ¹/₂ et ⁴/₃.

3) Résoudre:-3x-2≥2x+8.

-3x-2≥2x+8 soit -3x-2x≥8+2

On obtient: -5x≥10.

Finalement on a: x≤-2 (on change le sens car on divise par -5)

Les solutions de l'inéquation -3x-2≥2x+8 sont tous les nombres inférieurs ou égal à -2.

Cas particuliers:

1) Résoudre une équation du type: x²=a:

On envisage trois cas:

1) a est négatif, pas de solution (un carré est toujours positif).

2) a=0, une seule solution: le nombre 0.

3) a est positif, on se ramène à une équation du type:

(on reconnaît l'identité remarquable:a²-b²=(a-b)(a+b))

Donc les solutions sont les nombres √a et -√a .

Exemples:

1) x²=-4: cette équation n'a aucune solution.

2) x²=16: x²-16=x²-4²=(x-4)(x+4)=0.

L'équation a donc 2 solutions: -4 et 4.

2) Repérer le facteur commun et se ramener à une équation produit:

Méthode: factoriser une somme, c'est l'écrire sous la forme d'un produit de facteurs: on repère le facteur commun.

Exemple:

A=(x+1)(x+2)-2(x+2)=0.

1ére étape: on repère le facteur commun, soit (x+2).

On extrait (x+2) et on note: A=(x+2)[(x+1)-2]

On écrit plus simplement l'expression entre les crochets:

A=(x+2)(x-1).

3ième étape: résoudre A=0, ce qui revient à écrire x+2=0 ou x-1=0, soit x=-2 ou x=1 (car équation produit) .

L'équation A a deux solutions: -2 et 1.

Systèmes d'équations:

Définitions:

Un système de deux équations à deux inconnues est la donnée de deux équations de la forme ax+by=c:

Avec a, b et c des nombres donnés et x et y deux inconnues.

Résoudre un système de deux équations à deux inconnues, c'est déterminer, s'ils existent, tous les couples (x;y) qui vérifient chacune des deux équations.

Méthodes:

1) Résolution par substitution: choisir une des deux équations et exprimer une inconnue en fonction de l'autre; puis remplacer dans l'autre équation l'inconnue par la valeur trouvée auparavant.

Donc on obtient une équation à une seule inconnue que l'on résout; une fois sa valeur trouvée, on peut trouver la valeur de la seconde inconnue.

2) Résolution par combinaison: multiplier les équations par des nombres bien choisis afin que les coefficients de l'une des deux inconnues soient opposés dans les deux équations.

Additionner les deux équations et faire disparaître l'une des deux inconnues.

Résoudre l'équation trouvée à une inconnue; une fois l'inconnue déterminée, on la remplace dans une des deux équations et on trouve la seconde inconnue.

Dans les deux méthodes on vérifie les résultats obtenus et on conclue.

Exemples:

Fonctions affines et fonctions linéaires:

Définitions:

Soient a et b deux nombres donnés et f la fonction qui à x associe y.

1) Si y = ax + b, on dit que f est une fonction affine.

2) Si y = ax, on dit que f est une fonction linéaire.

Propriétés:

La représentation d'une fonction linéaire est une droite passant par l'origine.

La représentation d'une fonction affine est une droite passant par le point de coordonnées (0;b).

b représente l'ordonnée à l'origine et a le coefficient directeur de la droite.

Si a>0 la droite "monte" et si a<0 la droite "descend".

Si b>0 la droite passe au-dessus de l'origine du repère et si b<0 la droite passe au-dessous de l'origine du repère.

Coefficients directeurs:

La donnée des coordonnées de deux points appartenant à la droite permet de calculer le coefficient directeur:

A(x_A;y_A) et B(x_B;y_B) deux points distincts d'une droite (D):

Savoir faire:

1) Trouver l'image d'un nombre:

On remplace x par ce nombre dans l'expression de f(x).

2) Trouver l'antécédent d'un nombre:

On doit trouver le nombre x qui a pour image a: on résout f(x)=a.

3) Tracer une droite:

Pour tracer la représentation graphique d'une fonction f affine ou linéaire, il suffit de placer deux points de coordonnées (x;f(x)), puis il faut tracer cette droite qui passe par ces deux points (choisir des points "éloignés" pour la précision du tracé).

4) Vérifier si un point appartient à une droite:

Les coordonnées des points qui appartiennent à une droite, vérifient son équation.

Exemples:

1) f(x)=2x+1, l'image de 2 par f est: f(2)=2×2+1=5.

L'image de 2 par f est 5.

2) f(x)=2x+1, l'antécédent de 5 est: f(x)=2x+1=5.

On résout 2x+1=5 soit 2x=4 et donc x=2.

L'antécédent de 5 par f est 2.

3) Représentation graphique de la fonction f affine: f(x)=2x-3.

4) f(x)=2x-3.

Soit le point E de coordonnées (4;5),

Calculons 2x-3 pour x=4: 2×4-3=8-3=5.

Donc E est un point de cette droite.

Statistiques:

Vocabulaire:

Population: c'est l'ensemble des éléments que l'on étudie.

Le nombre total d'individus de la population est appelé effectif total et il est noté N.

Caractère d'une population: c'est la propriété de cette population que l'on étudie pour le calcul;

le caractère peut être qualitatif (exemples: couleurs des cheveux; le sport pratiqué;...) ou quantitatif (exemples: la taille; l'âge;...).

Effectif d'un caractère: c'est le nombre d'éléments qui possèdent un même caractère.

Valeur: les valeurs que peut prendre le caractère.

Fréquence:la fréquence d'une valeur est donnée par:

Moyenne:

La moyenne d'une série statistique est le quotient de la somme de toutes les valeurs de cette série par l'effectif total.

n₁, n₂, ... ,n_p : les effectifs.

On a: N=n₁+n₂+...+n_p.

x₁, x₂, ... ,x_p : les valeurs du caractère.

Moyenne:

Définition:

Etendue: L'étendue d'une série statistique est la différence entre la plus grande et la plus petite valeur de la série.

Plus l'étendue est élevée, plus la série est dispersée.

Définitions:

Médiane: on appelle médiane d'une série statistique ordonnée la valeur qui permet de séparer la série statistique en deux séries de même effectif:

1) une série ayant des valeurs du caractère toutes inférieures ou égales à la médiane;

2) l'autre série ayant des valeurs du caractère toutes supérieures ou égales à la médiane.

Quartiles:

On appelle premier quartile la plus petite valeur, notée Q₁, de la série telle qu'au moins un quart (25%) des valeurs soient inférieures ou égales à Q₁.

On appelle troisième quartile la plus petite valeur, notée Q₃, de la série telle qu'au moins trois quart (75%) des valeurs soient inférieures ou égales à Q₃.

Exemples:

1) 5-6-11-13-6-14-12-8-13: les 9 notes d'un élève en mathématiques lors du dernier trimestre.

Tout d'abord il faut ranger dans l'ordre croissant: 5-6-6-8-11-12-13-13-14.

Il y a 9 notes, or 9 est un nombre impair.

La médiane sera la 5ième valeur: la médiane est: M_e=11.

2) Pendant ce même trimestre, il a reçu 6 notes en sciences physiques:

6-13-18-16-14-5: or 6 est un nombre pair.

Il faut ranger dans l'ordre croissant: 5-6-13-14-16-18.

La médiane sera la moyenne de la 3ième et la 4ième valeur: la médiane est:

On en déduit qu'il y a autant d'élèves qui ont eu une note inférieure à 13,5 que d'élèves qui ont eu une note supérieure à 13,5.

3) Dans un stock de pièces métalliques, on donne leur longueur, exprimée en millimètres.

Ces longueurs sont rangées dans l'ordre croissant:

3-3-8-9-11-19-19-31-34-44-53-79: soit au total 12 valeurs.

^N/₄=¹²/₄=3; donc la premier quartile est Q₁=8 car c'est la 3ième valeur.

^3N/₄=^3×12/₄=36/₄=9; donc le troisième quartile est Q₃=34 car c'est la 9ième valeur.

Ce qui signifie qu'il y a 25% des pièces qui mesurent en-dessous de 8mm et 75% des pièces qui mesurent en-dessous de 34mm.

Probabilités:

L'univers, noté Ω, est l'ensemble de toutes les issues (résultats) qui peuvent être obtenus au cours d'une expérience aléatoire.

Définitions:

résultats à utiliser :issues, aléatoire et expérience.

Les résultats ou issues possibles d’une expérience aléatoire sont appelées éventualités.

Un évènement est un ensemble d’éventualités. Un événement est réalisé lorsque l’une des éventualités qui le compose est réalisée.

Une éventualité est un événement élémentaire.

* Un événement est impossible s'il ne peut pas se produire.

* Un événement est certain s'il se produit forcèment.

* Deux événements sont incompatibles s'ils ne peuvent se produire en même temps.

Propriétés:

1) La probabilité d'un événement est égale à la somme des probabilités qui réalisent cet événement.

2) La probabilité d'un événement impossible est égale à 0.

3) La probabilité d'un événement certain est égal à 1.

4) La probabilité d'un événement est un nombre compris entre 0 et 1.

5) L'événement contraire d'un évènement A se note à et correspond à la négation de l'événement A:

P(A)+p(Ã)=1 soit P(Ã)=1-P(A).

Définition:

mots à utiliser :équiprobabilité, aléatoire et chance.

Propriété:

Dans une situation d'équiprobabilité, la probabilité d'un événement A est le quotient du nombre des éléments de Ω correspondant à cet événement par le nombre total des éléments de Ω.

Exemple:

On lance une pièce de monnaie et on regarde la face obtenue.

Cette expérience est aléatoire : il y a 2 issues possibles : Pile ou Face

La pièce n'est pas truquée.

On lance la pièce une première fois et on note sa face, puis on la lance une seconde fois et on note la face.

Arbre pondéré:

La probabilité d'obtenir "Pile" au premier lancer et "Pile" au second est: P(pile, pile)=1/2×1/2=1/4. Avec un arbre, la probabilité de l’issue auquel conduit un chemin est égal au produit des probabilités rencontrées le long du chemin.

Thalès:

Théorème:

Si ABC est un triangle et (D) est une droite telle que:

(D) est parallèle à (BC)

(D) coupe (AB) en un point M et (AC) en un point N.

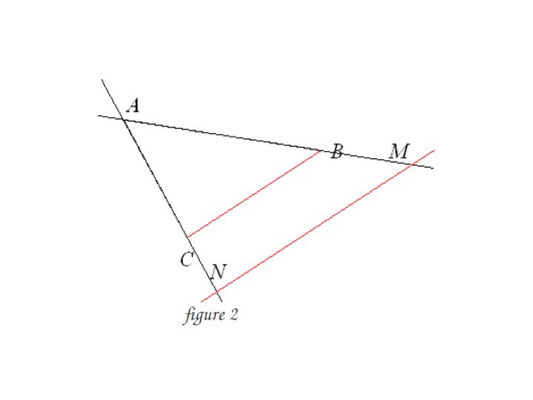
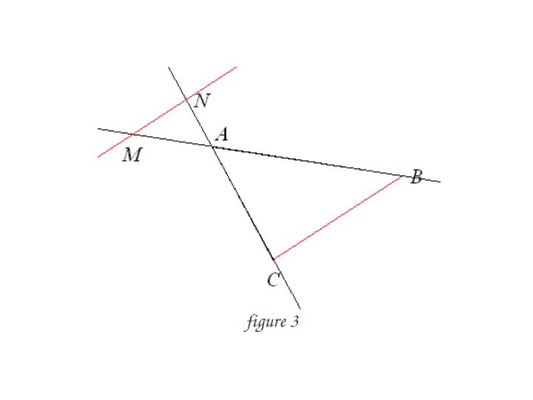
On se trouve alors dans le cas d'une des 3 figures ci-dessous, appelées: "configurations de Thalès".

Dans les trois cas, on a l'égalité suivante:

résultats à utiliser : ^AM/_AC = ^AN/_AB = ^MN/_BC; ^AM/_AB = ^AN/_AC = ^MN/_BC et ^AB/_AC = ^BC/_MN.

Réciproque du Théorème de Thalès:

Si ABC est un triangle et (D) est une droite telle que:

1) (D) coupe (AB) en un point M et (i) en un point N.

2) Les points A, M et B sont respectivement dans le même ordre que les points A, N et C.

3) ^AM/_AB=^AN/_AC.

Alors (D) est parallèle à (BC).

Utilisations: 2 types de questions:

1) Théorème de Thalès: il sert pour calculer des longueurs lorsqu'on a une configuration de Thalès.

2) Réciproque du Théorème de Thalès: elle sert pour démontrer le parallélisme de deux droites (on vérifie l'égalité entre deux rapports).

Exemples:

Trigonométrie:

Pour effectuer les calculs, on vérifie que la calculatrice est en DEGRÉ.

Cosinus, Sinus et Tangente: On travaille dans le triangle ABC rectangle en B. résultats à utiliser :(côté opposé)/hypothénuse; (côté opposé)/(côté adjacent) et (côté adjacent)/hypothénuse. 1) Cos  = . 2) Sin  = . 3) Tan  = . Vérifie tes réponses: 1) Cos Â=adjacent/hypothénuse=AB/AC 2) Sin Â=opposé/hypothénuse=BC/AC 3) Tan Â=opposé/adjacent=CB/AB

Astuce pour mémoriser: SOH CAH TOA.

sin=opp/hyp; cos=adj/hyp et tan=opp/adj

Propriétés:

Relations entre cosinus, sinus et tangente d'un angle aigu α:

1) cos²α+sin²α=1

2) tanα=^sinα/_cosα

Utilisations: 2 types de questions:

On travaille dans un triangle rectangle.

De plus, l'angle étant aigu, le sinus est compris entre 0 et 1.

1) Déterminer la valeur d'un angle aigu.

2) Déterminer une longureur.

Angles inscrits et polygones réguliers: